Physics Lab.2022 幾何班紹介 (Advent Calendar)

はじめに

こんにちは、物理学科3年のクレイ(粘土)と申します。

Physics Lab.2022では「幾何班」の班長を務めさせていただいています。 アドベントカレンダーの形式を借りて、この記事では幾何班の活動を紹介していきたいと思います。

幾何班とは？

幾何学について

本班ではシンプレクティック幾何学をはじめ、微分幾何学や位相幾何学、Lie群論などを扱う予定です。 よく「幾何学」というと、中高数学に出るような平面図形や作図、あるいはテセレーションを想像すると思いますが、私たちはそういうことはしません。 とは言っておきましたが、せっかくなので今挙げた「幾何学」の分野がどのように「中高数学の幾何学」と関連しているかを見ていきましょう。

中高数学の幾何学は、ユークリッド空間、つまり平坦な座標系が取れる空間での図形を扱います。ここで平坦な座標系というのは、各点での軸方向が正規直交していて、またベクトルを平行移動させたときに成分がそのまま移るなど、都合のいい性質を持っています。

しかし、同じ2次元でも平面ではなく球面だったらどうでしょうか？ベクトルの平行移動が移動した径路に依存するなど、ユークリッド空間の性質が成り立たなくなってしまいます。球面のような曲面を上では、平行移動を含め、ベクトル解析の勾配・発散・回転などの演算をまた新しく定義しなければならなくなります。つまりユークリッド幾何学より一般的な状況に適用できる幾何学が要求されるわけです。 そしてもう一つ、曲面上で幾何学をするには、その曲面が3次元空間に置かれていることを意識してもあまり役に立ちません。1 むしろその曲面に住んでいるアリになって「局所的には2次元平面で、平行移動や長さなどが点ごと異なる」という内部的な態度をとることで曲面の記述が簡単になります。それが微分幾何の始まりです。

幾何学をひとまとめに言うと、図形の「形」を扱う学問です。形というのは、解釈の仕方にもよりますが、基本的には見方やものさしによらない性質を指します。

微分幾何学の目標の一つは、幾何学(中でも特に局所的な部分)を、座標系に依存しない形で記述することです。 座標をまったく使わないという方法でもいいし、やむを得ず座標系を入れるとしても、座標系の取り方を替えても適切な変換則を与えて片方の記述を変換したものがもう片方の記述と一致するならば、そうやって直交座標だけでなく、斜交座標系だったり、曲がっていたりしても適用できるように一般的な座標系での記述を与えることができればokです。

幾何学のもう1つの分野はトポロジー(位相幾何学)です。トポロジーは局所的な各部分を合わせて全体を作ったとき、「合わせ方」に着目します。 例えば球面とドーナツ面(トーラス)は局所的にはどちらも2次元面ですが、全体としては違う形をしています。 表面に住んでいるアリには同じく見えますが、そのアリたちにも自分がどちらに住んでいるか調べることができます。 アリ1匹の両手に糸の両端を持たせて、そのアリが両端を持ったまま糸を引っ張って必ず糸全体を回収できるかを見ればいいです。

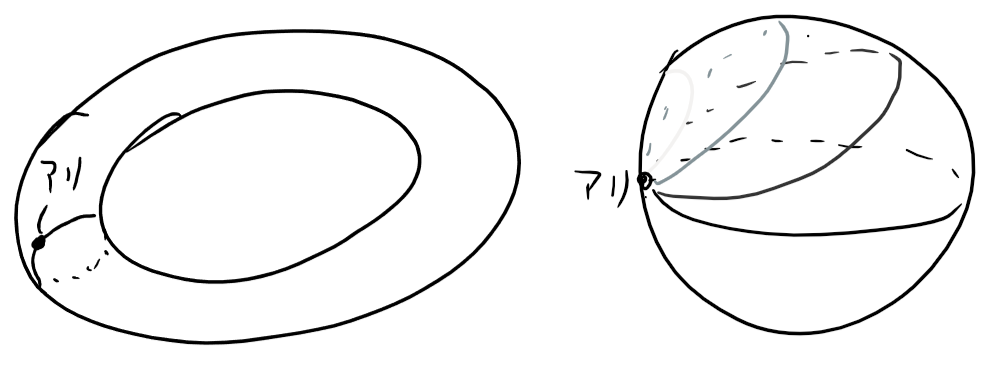
f:id:nendo_riggg:20211202235602p:plain

図のように、球面上のアリは必ず糸を回収できますが、トーラス上のアリは柱を一周する糸は回収できません。

ここまで言うとどこが物理学と関係あるのか分からないものですが、実は現代の理論物理学の発展は幾何学とその軌を一にしてきたと言って過言ではありません。物理学で大前提とする「物理法則は観察者やものさしによらない」普遍性は、まさに幾何的です。そして実際、物理学の所々に幾何学が現れています。

その代表例として相対論やゲージ理論があります。一般相対論は時空間の構造自体と物理との対応を、ゲージ理論では内部対称構造と物理との対応を示唆しています。極端に還元主義的に言うと、物理法則は幾何構造の法則になるわけです。

班の性格について

歴代のPhysics Lab.では実験メインの班が多かったのですが、コロナ禍によりすべてのPhysics Lab.がオンライン公開になった年からは純粋理論・数理物理寄りの班が立ち始めました。私たちの幾何班もその一つです。

その結果、今回の他班を見ると

「量子物理班」「トポロジカル物性班」「生物物理班」「宇宙班」

のように、どちらも実際の現象に直接突き詰めていて、ほとんどは手軽に実験もできる分野である半面、幾何班は少し異質的な存在になっていますね。

ちなみにトポロジカル物性班とはネタが被っています。幾何班としてはスピン構造や重力、ゲージ理論などと言った物理理論の数学的構造にフォーカスを当てるようにして差別化を図っています。幾何班の内容でも実験ができないわけではないですが、2幾何学だけでなく物性の知識も要求されるので、それこそ学部生の実験としてはハードルが高すぎると判断しています。

実験は行わないので、色んなテーマを自主ゼミで勉強し、展示に向けては勉強した内容を活かして一般人向けのポスターや解説記事を作成する予定です。形式としては、一つのテーマに絞って学科の2年生と3年生が分担して丁寧めの記事を書くか、複数のテーマに分けてより多様な記事を書くかのどちらかですが、まだ未定です。

テーマ詳細

候補案のテーマの詳細を説明したいと思います。 急いで書いたので数式も充分ではなく、また余計に詳細になってしまいましたが、なんとなく雰囲気だけ感じていただければと思います。

古典力学、熱力学

実は幾何班が立ったきっかけになったのは「シンプレクティック幾何学の自主ゼミ」でした。 古典解析力学の一つであるハミルトン力学での状態空間は位置 x と運動量 p との対 (x,p) という座標系で表せて、かつ x,p を対とする特殊な構造(反対称2形式 \omega )を与えることができますが、その構造がある空間をシンプレクティック空間といい、シンプレクティック幾何学の対象になります。古典力学はそのシンプレクティック空間とその上の関数 H (ハミルトニアン)により完全に定まります。

シンプレクティック空間が定まれば、その空間の上の古典力学を量子化して、量子力学を考えることができます。 これは量子化と言われるプロセスですが、シンプレクティック空間ならば位置・運動量からなる空間でなくても量子化することができます。これを幾何学的量子化と言います。 スピンはよく「古典論での対応が存在しない」と誤解されていますが、実は回転する3次元球面を量子化することで得ることもできます。

熱力学でも、接触構造という形でシンプレクティック構造が登場します。例えば体積 V と圧力 p が、温度 T とエントロピー S が対応するらしいです。

スピン

先ほども言ったように、スピンは量子論的な概念で、古典論では登場しないというよく誤解されますが、実は古典論のコンテキストでも登場しています。

電子のようなスピン1/2はローレンツ群が作用する最小表現(カイラルスピノル)としても現れて、さらに反対カイラルのスピノル2つを合わせると時空上の「クリフォード代数」というものによって変換されるものが出てきます。このクリフォード代数はディラックのガンマ行列と呼ばれるものになっています。いずれも量子化待ちの古典論です。

ゲージ理論

ゲージ理論は時空間の各点に内部自由度を持つ場に関する理論で、重力以外の基本相互作用はすべてゲージ理論によって説明されています。3

要は、ある内部自由度が与えられたときに、その基準点は各点において任意に設定することができます。その内部自由度の基準点が決まったら、各点の周りで内部自由度の基準点の変化率が決まります。その基準点の変化率をゲージ場と呼びます。ここまでは、ゲージ場には「もとの点に戻ったら変化率はゼロ」という制約が付きます。

次に、ゲージ場からその制約を外します。(これをゲージ化と呼びます。) そしてそのゲージ場が独立な対象としてゲージ場の項を入れると、ゲージ場自体の運動方程式が得られます。 その方程式はなんと、\mathrm{U}(1) ゲージ理論ではマックスウェル方程式と一致します。 他の内部自由度、例えば \mathrm{SU}(N) という対称性に関する理論はヤン＝ミルズ理論と呼ばれていて、その運動方程式もマックスウェル方程式にそっくりです。

電磁気学( \mathrm{U}(1) ゲージ理論 )においてこのゲージ場はスカラー \phi とベクトルポテンシャル \bm A です。そして、場の量子論によるとこのゲージ場を量子化したものは光子です。古典的にはただの計算上の概念に過ぎなかった磁気ポテンシャル \bm A は、ゲージ理論ではこのように物理的本質になります。

重力理論(一般相対論)

時空の曲がり具合は、ベクトルの長さを表す計量 g, そしてベクトルを平行移動させたときどれだけ変化するかを表す接続 \Gamma によって決まります。いくつかの要請のもとで \Gamma は g に依存します。 一般相対論は、その g と \Gamma を力学変数として重力を記述します。

一方、時間の曲がり具合を記述するには、多脚場と呼ばれるもう1つの方法があります。 各点で定義できる局所ローレンツ軸 e (多脚場)と、\Gamma と似た役割の \omega (スピン接続)で表現する方法です。 この e,\omega をもとに重力を記述する理論はカルタン重力と呼ばれます。

実は2つの表現は同等で、g,\Gamma は e,\omega で簡単に表せますが、その逆、つまり e,\omega を g,\Gamma で表すことは(存在はするが)難しく、余分の自由度もできるので、多脚場の方が一般的に扱いやすい形になっています。

加えて、カルタン重力理論の強みは、スピンとの結合を表現できるところにあります。スピンは各点のローレンツ軸でしか表現できない構造になっているので、スピノル場のある重力理論を記述するにはカルタン重力が必要です。

それだけでなく、実はここで定義した \omega が多脚場 e のローレンツ自由度におけるゲージ場になっていたり、その e をまた並進移動に対するゲージ場と解釈する立場もあったりします。 なお、重力がどのようにゲージ理論と関係しているかは、まだ明確ではありません。重力自体をゲージ理論として説明しようとする素朴な見解から、AdS/CFTから重力とゲージ理論の対応性が分かるという、もしくは散乱振幅上に重力がゲージ理論の二重コピーという理論まで様々な見解があります。

私個人的には二重コピー理論が面白そうに思いましたが、そこまで深入りするのは今はやめておきましょう。

それらと関係している何か

これらの理論が物理を説明する土台になることは間違いないですが、学部生のうちそれを勉強してさらにその内容を記事でまとめることになると、現実的に難しくなりますね。オチがあるところで切りたいし。

現在としては、アティヤ=シンガーの指数定理という定理を突き詰めてみようと思っています。 まだ勉強中ですが、この定理は多様体上で定義される微分方程式の解集合の特性を決定することに役立つらしいです。

余力があれば、指数定理がどのようにゲージ理論や重力理論、超対称性の解につながるかもやってみたいと思います。 もし目標の指数定理までたどり着けなかったとしても、そこまで勉強した記事のネタになるでしょう。(フラグ)

さいごに

偉そうに書いてはいましたが、恥ずかしながら班長の私はこれらの内容に関してはほぼ初心者です。 （少しでも背景知識があったら、もっとマシな記事が書けたと思います。また、以上の内容が不正確もしくは間違いがある可能性がありますので、ご了承ください。）

特に、これらの内容で本当の意味で物理をするためにはカオス系や場の量子論など膨大な理論を勉強しなければならず、班員ともに頑張ってはいるものの、タイトな学科授業と同時進行することの大変さをしみじみと感じています。現時点では、ただ数式の美しさを鑑賞するレベルにとどまっても上出来かな、と思います。

最近はトポロジカル絶縁体の発見により、物性のような身近な分野でもトポロジーの重要性が浮き彫りになっています(現に、Physics Lab.2022にはトポロジカル物性班が別途に立っています)が、勉強途中の学部生という面もあり、本班では数学的な記述にフォーカスを当てるようにしています。

ただ、初心者だからこそ初心者目線で解説記事が書けるのではないか、と私個人的には期待しています。 物理非専攻や高校生の方々にも、どうか楽しみにしていただけると幸いです。 至らない点は多々あるかと思いますが、Physics Lab.2022のこと、幾何班を何卒よろしくお願いします。

参考文献

  1. 実は、まったく意味がないわけではありません。例えば Anti-de Sitter空間と呼ばれる特殊な曲がった時空間は、「時間軸」をもう1つ加えて平坦な時空間として扱うことがしばしばあります。ただしその場合でも、もう1つの次元が物理的実体があるというより、あくまでも計算上のツールとして導入している印象ですね。なお、Anti-de Sitter空間は最近話題のAdS/CFT対応(Anti-de Sitter空間・共形場理論対応)で認知されています。↩

  2. 後述する指数定理も、超電導現象を用いて実験的検証ができるそうです。↩

  3. ただし、どのような内部自由度があるかは疑問の余地があります。電磁気と弱い相互作用は [tex:\mathrm{SU}(2)\times \mathrm{U}(1)Y] ゲージで表され、低温ではこの対称性が破れます。強い相互作用(色力学)は \mathrm{SU}(3) ゲージで表されます。それらを独立な自由度と見るのが標準模型、[tex:\mathrm{SU}(3) \times \mathrm{SU}(2)\times \mathrm{U}(1)Y] 相互作用ですが、最近は標準模型からずれている観測結果も発表されています。)↩